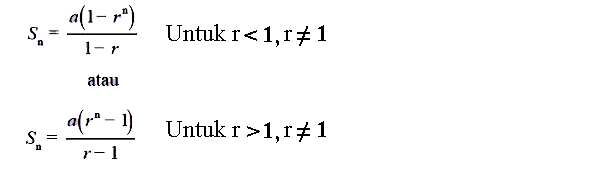Matematika adalah salah satu disiplin ilmu yang kaya akan pola dan struktur. Pemahaman tentang pola bilangan dan ruang-ruang dalam matematika sangat penting, karena ini tidak hanya membantu dalam menyelesaikan masalah-masalah aritmetika, tetapi juga dalam mengembangkan keterampilan berpikir logis dan analitis. Artikel ini akan menguraikan sepuluh jenis pola bilangan dan ruang-ruang dalam matematika yang sering muncul dan memiliki aplikasi penting dalam berbagai cabang ilmu, baik dalam teori maupun praktik.
Berikut adalah sepuluh jenis pola bilangan dan ruang-ruang dalam matematika:
- Pola Bilangan Aritmetika: Pola ini merupakan deret bilangan yang diperoleh dengan menambahkan bilangan tetap pada setiap suku. Contohnya adalah 2, 4, 6, 8, dan seterusnya, di mana selisih antar suku adalah 2.
- Pola Bilangan Geometri: Pola ini muncul ketika setiap suku diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap. Misalnya, deret 3, 6, 12, 24 yang diperoleh dengan mengalikan setiap suku dengan 2.
- Pola Bilangan Segitiga: Pola ini terdiri dari bilangan berturut-turut yang dapat membentuk bentuk segitiga. Contohnya adalah 1, 3, 6, 10, dan seterusnya, di mana setiap suku dapat dinyatakan sebagai jumlah dari deret bilangan bulat positif.
- Pola Bilangan Persegi: Angka dalam pola ini adalah hasil dari pengkuadratan bilangan bulat. Contohnya termasuk 1, 4, 9, 16, yang merupakan kuadrat dari 1, 2, 3, dan 4.
- Pola Bilangan Fibonacci: Pola ini terkenal dalam banyak konteks, termasuk dalam alam. Bilangan Fibonacci dimulai dari 0 dan 1, lalu setiap suku berikutnya merupakan jumlah dari dua suku sebelumnya, sehingga deretnya adalah 0, 1, 1, 2, 3, 5, 8, 13, dan seterusnya.
- Pola Bilangan Prime (Bilangan Prima): Bilangan prima adalah bilangan yang lebih besar dari 1 dan hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Contohnya adalah 2, 3, 5, 7, 11, dan 13. Polanya sangat penting dalam teori bilangan dan kriptografi.
- Pola Bilangan Genap dan Ganjil: Pola ini mengelompokkan bilangan menjadi dua kategori. Bilangan genap adalah semua bilangan yang habis dibagi 2, sedangkan bilangan ganjil adalah bilangan yang tidak habis dibagi 2. Contoh bilangan genap: 0, 2, 4, 6; contoh bilangan ganjil: 1, 3, 5, 7.
- Pola Bilangan Kuadrat Magis: Dalam pola ini, jumlah angka di setiap baris, kolom, dan diagonal sama. Bilangan kuadrat magis sering kali disusun dalam bentuk kotak, dengan angka terpisah sedemikian rupa untuk menjaga keseimbangan.
- Pola Bilangan Faktorial: Pola ini melibatkan hasil kali dari semua bilangan bulat positif hingga n, dinyatakan sebagai n!. Contohnya, 0! = 1, 1! = 1, 2! = 2 x 1 = 2, 3! = 3 x 2 x 1 = 6, dan seterusnya. Faktorial memiliki banyak aplikasi dalam kombinatorika.
- Pola Bilangan Deret Harmonik: Dalam pola ini, suku berikutnya adalah invers dari bilangan bulat positif. Misalnya, deret tersebut adalah 1, 1/2, 1/3, 1/4, dan sebagainya. Deret ini memiliki aplikasi dalam teori musik dan fisika.
Kesepuluh jenis pola bilangan dan ruang-ruang ini memberikan kerangka kerja yang mendalam untuk memahami struktur matematika. Mereka tidak hanya berfungsi sebagai alat untuk menyelesaikan masalah, tetapi juga sebagai cara untuk menghasilkan gagasan baru dan mempromosikan kreativitas. Mengkaji dan mengenali pola-pola ini dapat berperan penting dalam berbagai aspek kehidupan, mulai dari pendidikan hingga penelitian ilmiah.
Selain itu, mempelajari pola bilangan dan ruang-ruang memberikan fondasi bagi konsep-konsep lebih lanjut dalam matematika, seperti fungsi, limit, dan struktur aljabar. Dengan demikian, memahami pola-pola ini dapat membantu individu mengembangkan rasa ingin tahu dan kecintaan terhadap matematika secara lebih mendalam.
Dengan mengenali dan mempelajari pola bilangan dan ruang-ruang yang ada dalam matematika, kita dapat memperluas wawasan kita mengenai ilmu ini. Semakin kita mendalami, semakin kita menyadari bahwa matematika bukan hanya sekadar angka, tetapi sebuah bahasa universal yang menggambarkan realitas di sekitar kita. Rasa ingin tahu yang kita tanamkan melalui pola-pola ini akan memfasilitasi proses pembelajaran yang lebih menyenangkan dan produktif di masa depan.