Pola bilangan merupakan salah satu konsep dasar dalam matematika yang membantu kita memahami keteraturan dan hubungan antara angka. Dalam kehidupan sehari-hari, kita seringkali menemui berbagai pola bilangan yang dapat digunakan untuk memecahkan berbagai masalah. Artikel ini akan membeberkan 10 jenis pola bilangan beserta gambarnya dan rumusnya, yang diharapkan dapat memberikan wawasan yang lebih dalam tentang pola bilangan tersebut serta aplikasinya dalam matematika.
- Pola Bilangan Aritmatika
Pola bilangan ini dihasilkan dengan menambahkan bilangan tetap (selisih) pada suku sebelumnya. Selain itu, rumus suku ke-n dapat ditulis sebagai:
an = a1 + (n – 1)d
- Pola Bilangan Geometris
Pola bilangan geometris diperoleh dengan mengalikan bilangan tetap (rasio) pada suku sebelumnya. Rumus suku ke-n untuk pola ini dapat dituliskan sebagai:
an = a1 × r(n-1)
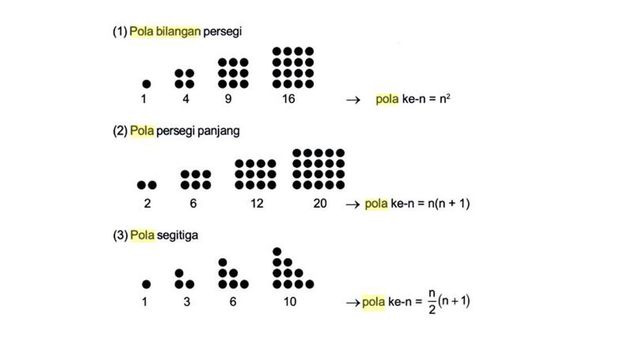
- Pola Bilangan Kuadrat
Pola bilangan ini memiliki suku-suku yang merupakan bilangan kuadrat dari angka bulat. Rumus untuk suku ke-n adalah:
an = n2
- Pola Bilangan Kubik
Pola ini melibatkan bilangan kubik, di mana setiap suku adalah kubus dari angka bulat. Rumus untuk suku ke-n adalah:
an = n3
- Pola Bilangan Fibonacci
Pola bilangan Fibonacci adalah urutan di mana setiap suku adalah hasil penjumlahan dari dua suku sebelumnya. Rumus untuk suku ke-n dapat dituliskan sebagai:
an = an-1 + an-2
- Pola Bilangan Segitiga
Pola ini melibatkan bilangan yang membentuk segitiga, yang merupakan jumlah suku tertentu. Rumus untuk suku ke-n adalah:
an = n(n + 1)/2
- Pola Bilangan Persegi Panjang
Pola bilangan ini dapat dilihat sebagai bilangan yang menghasilkan area persegi panjang. Rumus untuk suku ke-n adalah:
an = n(n + 1)
- Pola Bilangan Genap
Pola bilangan genap terdiri dari bilangan-bilangan yang dapat dibagi dua tanpa sisa. Rumus untuk suku ke-n adalah:
an = 2n
- Pola Bilangan Ganjil
Pola bilangan ganjil terdiri dari bilangan yang memiliki sisa satu ketika dibagi dua. Rumus untuk suku ke-n adalah:
an = 2n – 1
- Pola Bilangan Deret Harmonik
Deret harmonik adalah pola di mana setiap suku merupakan invers dari bilangan bulat. Rumus untuk suku ke-n adalah:
an = 1/n
Dengan memahami berbagai jenis pola bilangan ini, kita dapat menggunakan pengetahuan matematika untuk memecahkan masalah yang kompleks dan menerapkannya dalam berbagai konteks. Setiap pola memiliki karakteristik dan rumus tersendiri, yang dapat kita eksplorasi lebih dalam dan manfaatkan dalam kegiatan sehari-hari. Mari kita terus menggali dunia matematika untuk menemukan lebih banyak pola dan aplikasinya dalam kehidupan. Semoga informasi ini bermanfaat bagi Anda yang sedang mempelajari pola bilangan dan cara kerjanya.