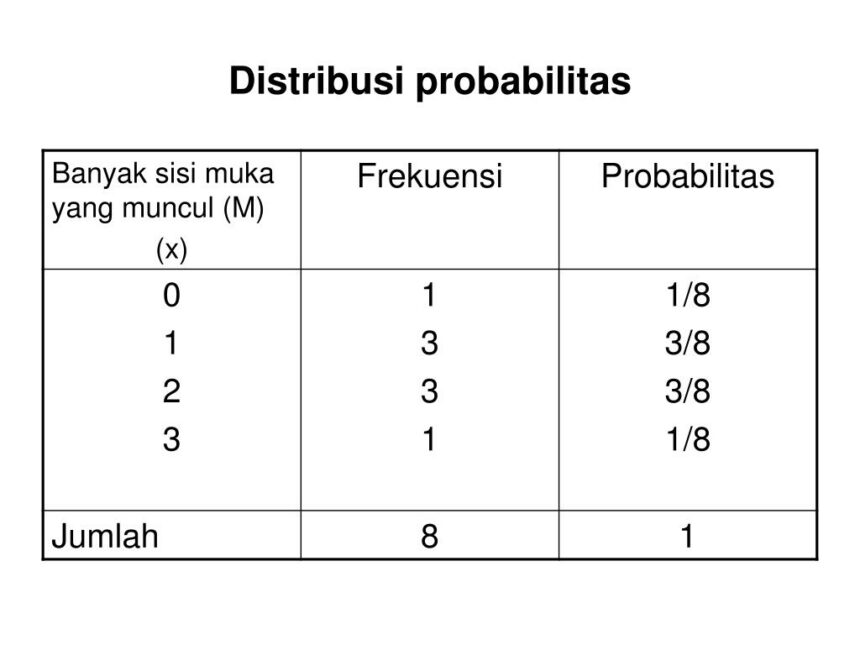
Statistika memainkan peran yang sangat penting dalam analisis data, dan salah satu konsep kunci yang perlu dipahami adalah distribusi probabilitas. Distribusi probabilitas menggambarkan bagaimana kemungkinan suatu variabel acak dapat berdistribusi. Dengan memahami berbagai distribusi probabilitas, individu dapat membuat inferensi yang lebih baik dari data yang ada, serta melakukan analisis yang lebih mendalam terhadap fenomena yang sedang diteliti. Dalam artikel ini, kita akan membahas 10 distribusi probabilitas dalam statistika yang wajib diketahui untuk meningkatkan pemahaman dan penerapan dalam analisis statistik.
Berikut adalah 10 distribusi probabilitas yang penting dan sering digunakan dalam statistika:
- Distribusi Normal: Distribusi ini sangat penting dalam statistik karena banyak fenomena alam mengikuti pola distribusi normal. Karakteristik utama dari distribusi ini adalah bentuk loncengnya dan simetrinya. Rata-rata, median, dan modus dari distribusi normal memiliki nilai yang sama.
- Distribusi Binomial: Distribusi ini digunakan ketika kita mengamati jumlah keberhasilan dalam sejumlah percobaan independen yang memiliki dua kemungkinan hasil (sukses atau gagal). Parameter yang digunakan adalah n (jumlah percobaan) dan p (probabilitas sukses dalam setiap percobaan).
- Distribusi Poisson: Distribusi ini digunakan untuk menghitung jumlah kejadian dalam interval waktu atau ruang yang tetap, di mana kejadian tersebut terjadi dengan rata-rata tetap dan independen. Distribusi Poisson sering digunakan dalam analisis jumlah kejadian, seperti jumlah panggilan ke pusat layanan dalam satu jam.
- Distribusi Eksponensial: Distribusi ini sering digunakan untuk memodelkan waktu antara kejadian dalam proses Poisson. Parameter dari distribusi ini adalah laju peristiwa, dan distribusi ini dapat digunakan untuk memperkirakan waktu hingga kejadian tertentu terjadi.
- Distribusi Geometrik: Distribusi geometrik mengukur jumlah percobaan yang diperlukan hingga keberhasilan pertama terjadi. Ini adalah distribusi yang digunakan dalam situasi di mana hasil dapat dianggap sebagai serangkaian percobaan yang mandiri.
- Distribusi Negatif Binomial: Distribusi ini merupakan generalisasi dari distribusi geometrik dan digunakan untuk menghitung jumlah percobaan yang diperlukan untuk mencapai sejumlah keberhasilan tetap. Ini berguna dalam situasi di mana kita ingin mengetahui seberapa banyak percobaan yang harus dilakukan untuk mencapai beberapa keberhasilan dalam percobaan berulang.
- Distribusi Gamma: Distribusi ini mencakup distribusi eksponensial dan distribusi Chi-squared. Distribusi gamma sering digunakan dalam situasi yang melibatkan waktu atau ukuran, dan dapat digunakan untuk memodelkan waktu hingga beberapa kejadian yang terjadi.
- Distribusi Chi-Squared: Distribusi ini digunakan dalam analisis varians dan uji independensi. Distribusi ini menghitung variansi sampel dan sering digunakan dalam pengujian hipotesis serta analisis frekuensi nominal.
- Distribusi T-Student: Distribusi ini digunakan dalam pengujian hipotesis untuk rata-rata ketika ukuran sampel kecil dan varians populasi tidak diketahui. Distribusi T memiliki lebih banyak probabilitas untuk nilai ekstrem dibandingkan distribusi normal, sehingga berguna dalam situasi di mana data tidak sepenuhnya mendekati normal.
- Distribusi F: Distribusi ini digunakan untuk membandingkan variansi dari dua sampel dan dalam analisis varians (ANOVA). Ini membantu dalam pengujian hipotesis tentang perbedaan rata-rata antara lebih dari dua kelompok.
Setiap distribusi di atas memiliki karakteristik unik dan penerapan tertentu dalam statistika. Memahami masing-masing distribusi ini penting untuk melakukan pemodelan statistik yang akurat dan untuk memahami sifat data yang sedang dianalisis. Misalnya, distribusi normal sangat vital dalam inferensi statistik dan pengujian hipotesis, sedangkan distribusi Poisson dan eksponensial sangat berguna dalam analisis data yang bersifat waktu.
Dalam praktiknya, analisis distribusi probabilitas dapat memberikan wawasan yang lebih dalam terhadap pola dan tren dalam data. Dengan menggunakan distribusi yang tepat, analisis dapat menjadi lebih akurat, dan keputusan yang diambil berdasarkan data tersebut akan lebih valid. Data yang dianalisis menggunakan distribusi probabilitas juga dapat mengarah pada pemodelan prediktif yang lebih kuat, yang bermanfaat dalam banyak area, dari bisnis hingga ilmu sosial.
Di dunia yang terus berkembang ini, kemampuan untuk memahami dan menggunakan distribusi probabilitas dalam analisis data menjadi semakin penting. Seiring dengan semakin kompleksnya big data, pemahaman yang baik tentang distribusi ini akan memungkinkan para profesional untuk menarik kesimpulan yang lebih signifikan dan mengambil keputusan yang lebih baik berdasarkan data.
Dengan demikian, menguasai 10 distribusi probabilitas yang telah dibahas adalah langkah awal yang krusial bagi setiap orang yang ingin mendalami statistik secara mendalam. Baik bagi akademisi, peneliti, maupun praktisi di industri, memahami distribusi ini bukan hanya akan membantu dalam analisis data yang berkualitas, tetapi juga dalam menciptakan solusi yang berbasis bukti untuk tantangan yang dihadapi dalam pekerjaan sehari-hari.