Dalam dunia matematika, pola bilangan sangat penting untuk dipahami, karena pola-pola ini membantu dalam memecahkan berbagai jenis masalah serta dalam memahami konsep yang lebih kompleks. Sebagian besar orang mungkin tanpa sadar sudah mengenal beberapa pola bilangan dalam kehidupan sehari-hari mereka. Melalui artikel ini, kita akan menjelajahi sepuluh macam pola bilangan dan aplikasi praktisnya dalam matematika. Dengan pemahaman yang lebih mendalam mengenai pola-pola ini, kita dapat meningkatkan kemampuan analitis dan pemecahan masalah kita.
Pola bilangan dapat ditemukan di berbagai bidang, mulai dari aritmetika dasar hingga geometri dan analisis. Memahami pola bilangan bukan hanya berguna bagi pelajar; profesional di bidang sains, teknik, dan ekonomi pun sering kali menggunakan pola ini untuk membantu mereka membuat prediksi dan keputusan yang lebih baik. Mari kita simak lebih lanjut mengenai macam-macam pola bilangan dan aplikasinya.
- Pola Bilangan Genap dan Ganjil
Bilangan genap adalah bilangan yang dapat dibagi oleh 2 tanpa sisa, sedangkan bilangan ganjil adalah bilangan yang tidak dapat dibagi oleh 2. Pola ini digunakan dalam pengalokasian sumber daya, alokasi waktu, dan dalam berbagai situasi di mana pembagian yang setara diperlukan. - Pola Bilangan Aritmetika
Pola bilangan ini terbentuk dengan menambahkan suatu bilangan tetap pada setiap suku. Contohnya, deret 2, 5, 8, 11, dengan selisih 3. Aplikasi pola ini mencakup penghitungan pertumbuhan populasi dan perencanaan biaya. - Pola Bilangan Geometri
Dalam pola ini, setiap suku diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap. Contohnya, 3, 6, 12, 24, yang masing-masing didapatkan dengan mengalikan 2. Pola ini berguna dalam analisis investasi dan pertumbuhan eksponensial. - Pola Bilangan Fibonacci
Deret Fibonacci dimulai dengan 0 dan 1, di mana setiap suku berikutnya adalah jumlah dua suku sebelumnya. Contohnya, 0, 1, 1, 2, 3, 5, 8. Aplikasi pola ini banyak ditemukan dalam seni, arsitektur, dan juga dalam biologi, seperti pola pertumbuhan daun. - Pola Bilangan Kuadrat
Bilangan kuadrat adalah hasil dari suatu bilangan yang dikalikan dengan dirinya sendiri. Contohnya, 1, 4, 9, 16, 25. Pola ini digunakan dalam geometri untuk menghitung luas dan juga dalam analisis algoritma dalam ilmu komputer. - Pola Bilangan Segitiga
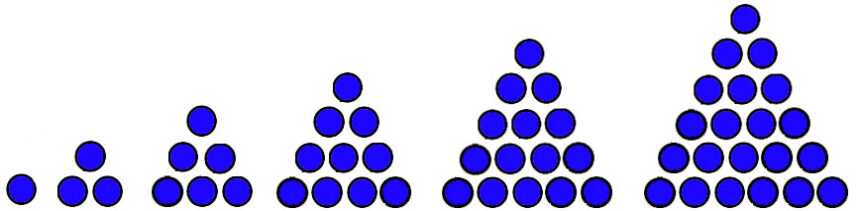
Bilangan segitiga dihasilkan dengan menjumlahkan angka-angka berturut-turut. Contohnya, 1, 3, 6, 10, 15. Pola ini berfungsi dalam kombinatorika untuk menghitung kombinasi atau jumlah kombinasi dari objek yang diambil. - Pola Bilangan Matriks
Pola ini melibatkan pengaturan bilangan dalam bentuk matriks. Dalam matematika terapan, pola matriks digunakan dalam transformasi dan pemodelan dalam berbagai disiplin ilmiah termasuk statistika dan ekonomi. - Pola Bilangan Pertambangan
Terkait dengan konsep probability dan statistik, pola ini digunakan dalam pengambilan keputusan dalam pengelolaan sumber daya dan penjadwalan. Aplikasi pola ini terlihat dalam riset operasional dan manajemen proyek. - Pola Bilangan Suku-Campuran
Menggabungkan bilangan bulat dan pecahan dalam deret. Contohnya, 1, 2.5, 4, 5.5, 7. Dalam dunia nyata, pola ini dapat digunakan dalam perhitungan uang, pengukuran, dan pembuatan skala. - Pola Bilangan Desimal
Pola ini melibatkan penggunaan sistem bilangan desimal, yang umum digunakan dalam aritmetika. Konsep pola ini sangat penting dalam perhitungan keuangan, pengukuran, dan analisis data.
Pola-pola bilangan yang telah dibahas di atas tidak hanya bermanfaat dalam konteks akademis, tetapi juga memiliki aplikasi nyata dalam kehidupan sehari-hari. Mampu mengenali dan memahami pola-pola ini dapat meningkatkan keahlian kita di berbagai bidang, baik dalam pekerjaan maupun studi. Dengan demikian, kita dapat lebih efektif dalam menghadapi berbagai tantangan yang mengharuskan kita untuk berpikir logis dan analitis.
Dengan memahami pola bilangan dan aplikasinya dalam matematika, kita membuka jalan bagi pengembangan kemampuan kognitif yang lebih baik. Setiap pola penting untuk dipahami karena mereka memiliki aplikasi unik dan relevansi di dunia nyata. Semoga artikel ini memberi wawasan yang lebih luas tentang pentingnya pola bilangan dalam matematika serta aplikasi praktisnya. Mari kita terus eksplorasi dan belajar lebih dalam mengenai keajaiban yang dihadirkan oleh matematika.