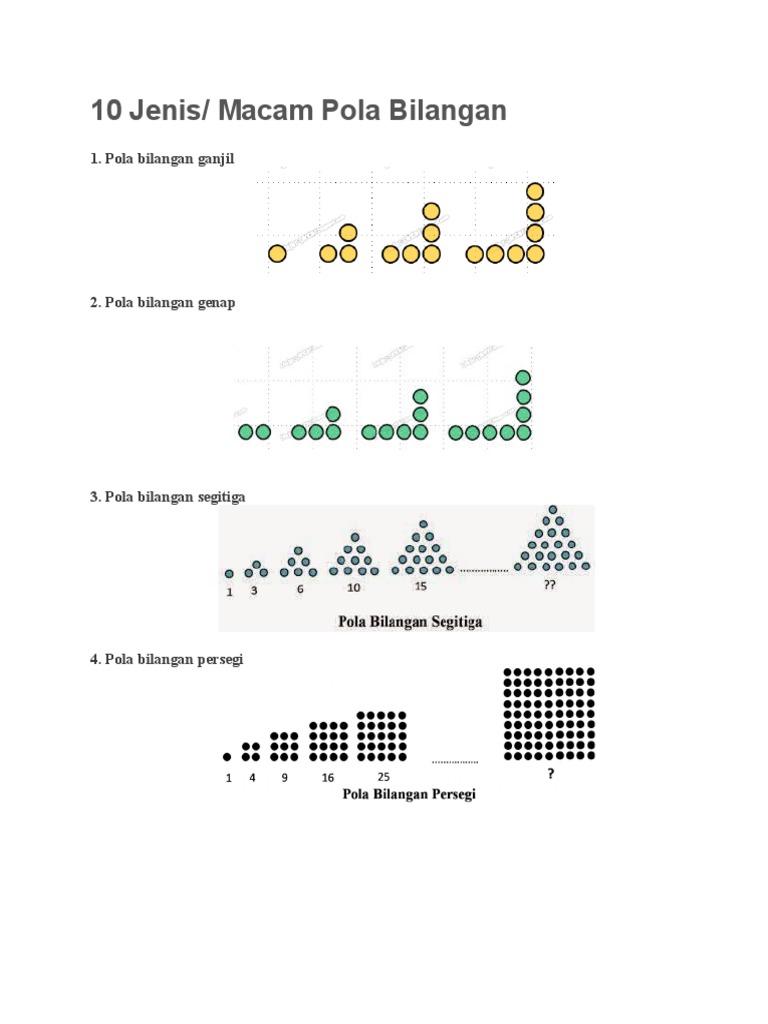
Pola bilangan merupakan suatu konsep yang penting dalam matematika, terutama dalam analisis data dan pengembangan metode pemecahan masalah. Setiap pola memiliki karakteristik dan aturan yang unik, yang sering kali digunakan untuk memecahkan berbagai permasalahan dalam matematika dan sains. Dalam artikel ini, kami akan membahas sepuluh jenis pola bilangan yang sering ditemukan, memberikan wawasan yang lebih dalam mengenai masing-masing pola tersebut.
Pola bilangan dapat membantu kita dalam berbagai aspek, mulai dari perhitungan sederhana hingga aplikasi yang lebih kompleks, seperti dalam algoritma komputer dan model matematis. Mari kita simak sepuluh jenis pola bilangan berikut yang dapat memperluas pemahaman kita tentang pola-pola ini:
- Pola Bilangan Aritmetika
Pola ini dibentuk dengan menambahkan bilangan tetap pada suatu angka. Contohnya adalah deret 2, 4, 6, 8, 10, di mana setiap angka bertambah dua. - Pola Bilangan Geometri
Pola ini terbentuk dengan mengalikan bilangan tetap. Contohnya adalah deret 3, 9, 27, 81, di mana setiap angka merupakan hasil kali dari bilangan sebelumnya dengan tiga. - Pola Bilangan Kuadrat
Deret ini terdiri dari bilangan kuadrat dari bilangan bulat. Contoh pola ini adalah 1, 4, 9, 16, 25, di mana setiap angka adalah hasil kuadrat dari bilangan bulat 1 hingga 5. - Pola Bilangan Kubik
Sama halnya dengan pola kuadrat, namun dalam bentuk angka kubik. Contohnya adalah 1, 8, 27, 64, 125, yang merupakan hasil kubik dari bilangan bulat 1 hingga 5. - Pola Bilangan Fibonacci
Deret ini dimulai dengan 0 dan 1, di mana angka berikutnya diperoleh dari penjumlahan dua angka sebelumnya. Contohnya adalah 0, 1, 1, 2, 3, 5, 8, 13, 21. - Pola Bilangan Segi banyak
Pola ini berkaitan dengan jumlah titik yang membentuk bentuk geometri tertentu. Misalnya deret segitiga 1, 3, 6, 10, 15, yang menunjukkan jumlah titik dalam bentuk segitiga. - Pola Bilangan Prima
Pola ini terdiri dari bilangan yang hanya memiliki dua pembagi, yaitu 1 dan bilangan itu sendiri. Contoh bilangan prima adalah 2, 3, 5, 7, 11, 13. - Pola Bilangan Genap dan Ganjil
Pola ini terdiri dari bilangan genap yang habis dibagi dua dan bilangan ganjil yang tidak. Contoh deret genap adalah 0, 2, 4, 6, dan deret ganjil adalah 1, 3, 5, 7. - Pola Bilangan Berurutan
Pola ini terbentuk dari bilangan yang disusun dalam urutan bertambah. Contoh deret ini adalah 1, 2, 3, 4, 5, dan seterusnya. - Pola Bilangan Berlaku
Pola ini diperoleh dari penjumlahan atau pengurangan bilangan sebelumnya dengan angka tertentu. Contoh deret ini adalah 10, 20, 30, 40, di mana setiap angka ditambahkan dengan sepuluh.
Dengan memahami berbagai jenis pola bilangan ini, seseorang dapat meningkatkan kemampuan analitisnya serta menerapkan pengetahuan ini dalam berbagai bidang. Setiap pola memiliki aplikasi dan relevansi yang berbeda, baik dalam kehidupan sehari-hari maupun dalam bidang akademik dan profesional. Misalnya, pola bilangan Fibonacci sering dipakai dalam permodelan pertumbuhan populasi, sementara bilangan prima memainkan peran penting dalam kriptografi dan keamanan data.
Ketika kita berlatih dengan berbagai jenis pola ini, kita tidak hanya memperkuat pemahaman kita tentang angka dan perhitungan, tetapi juga belajar cara berpikir logis dan sistematis. Terlebih lagi, pemahaman tentang pola bilangan ini juga memiliki dampak positif dalam pemecahan masalah yang kompleks, di mana pengenalan pola dapat memberikan wawasan yang lebih jelas.
Secara keseluruhan, pola bilangan adalah salah satu elemen penting dalam matematika yang membentuk dasar dari banyak teori dan aplikasi. Dengan eksplorasi lebih lanjut tentang sepuluh jenis pola bilangan ini, diharapkan akan lebih banyak orang yang terinspirasi untuk mengeksplorasi matematika dan melihat nilai praktisnya dalam kehidupan sehari-hari.
Secara ringkas, berkenalan dengan berbagai pola bilangan membantu kita dalam mengembangkan keterampilan berpikir logis, serta memberikan perspektif baru dalam memahami konsep-konsep matematis yang lebih kompleks. Akhir kata, seperti halnya dalam banyak aspek kehidupan, memahami dasar-dasar matematika, termasuk pola bilangan, akan membawa kita pada pemahaman yang lebih dalam dan kemampuan untuk menerapkannya dengan cara yang lebih efektif.