Matematika merupakan salah satu disiplin ilmu yang tidak hanya berfungsi dalam perhitungan, tetapi juga dalam menggambarkan dan memahami berbagai bentuk dan struktur. Dalam dunia geometri, banyak sekali bangun datar yang memiliki karakteristik dan sifat tersendiri. Mengetahui bangun datar ini sangat penting, baik dalam pendidikan dasar maupun dalam aplikasi sehari-hari. Artikel ini akan membahas sepuluh bangun datar yang sering kita temui dalam matematika. Dengan pemahaman yang lebih baik mengenai setiap bentuk ini, diharapkan pembaca dapat menghargai keindahan dan keteraturan dalam geometri.
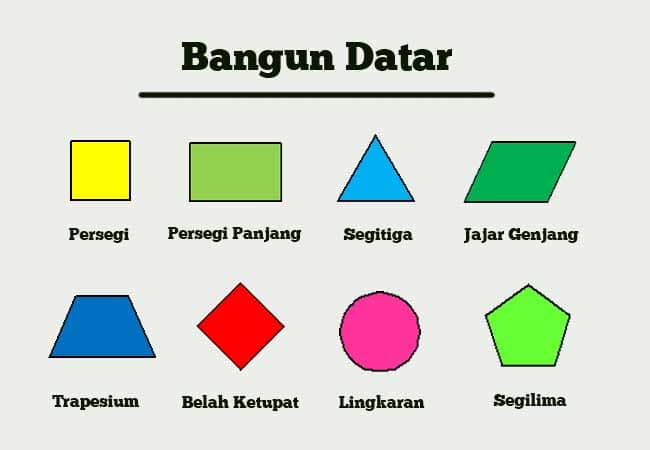
- Persegi
Persegi adalah bangun datar dua dimensi yang memiliki empat sisi dengan panjang yang sama. Setiap sudut pada persegi adalah sudut siku-siku (90 derajat). Luas persegi dapat dihitung dengan rumus L = s x s, di mana s adalah panjang sisi. Contoh dari persegi dapat kita lihat pada ubin lantai dan layar komputer.
- Persegi Panjang
Persegi panjang mirip dengan persegi, namun memiliki dua sisi yang lebih panjang dan dua sisi lainnya yang lebih pendek. Semua sudut pada persegi panjang juga merupakan sudut siku-siku. Luasnya dapat dihitung dengan rumus L = p x l, di mana p adalah panjang dan l adalah lebar. Persegi panjang sering kita temui dalam bentuk meja, papan, dan juga layar televisi.
- Segitiga
Segitiga merupakan bangun datar yang memiliki tiga sisi dan tiga sudut. Terdapat berbagai jenis segitiga, antara lain segitiga siku-siku, segitiga sama kaki, dan segitiga sama sisi, masing-masing dengan sifat dan rumus luasnya sendiri. Luas segitiga dapat dihitung dengan rumus L = (alas x tinggi) / 2. Segitiga banyak ditemui dalam desain arsitektur dan struktur bangunan.
- Lingkaran
Lingkaran adalah bangun datar yang memiliki semua titik pada jarak yang sama dari pusat. Panjang keliling lingkaran dapat dihitung dengan rumus K = 2πr, di mana r adalah jari-jari. Luasnya dapat dihitung dengan L = πr². Lingkaran dapat kita temui dalam berbagai objek sehari-hari, seperti roda sepeda dan piringan.
- Jajargenjang
Jajargenjang adalah bangun datar dengan dua pasang sisi yang sejajar dan sama panjang. Sudut-sudut pada jajargenjang tidak selalu siku-siku. Luas jajargenjang dapat dihitung dengan rumus L = alas x tinggi. Contoh jajargenjang dapat kita jumpai dalam bentuk sengkang pada atap rumah.
- Trapesium
Trapesium adalah bangun datar yang memiliki sepasang sisi sejajar. Jenis-jenis trapesium termasuk trapesium sama kaki dan trapesium siku-siku. Luas trapesium dapat dihitung dengan rumus L = (a + b) / 2 x tinggi, di mana a dan b adalah panjang sisi sejajar. Trapesium sering digunakan dalam desain grafis dan arsitektur.
- Belah Ketupat
Belah ketupat adalah bangun datar yang memiliki empat sisi sama panjang dan dua pasang sudut yang sama besar. Luas belah ketupat dapat dihitung dengan rumus L = (d1 x d2) / 2, di mana d1 dan d2 adalah panjang diagonal. Belah ketupat sering muncul dalam kerajinan tangan dan seni.
- Overlapping Squares
Meskipun tidak dikenal secara luas dalam kurikulum formal, bangun overlapping squares adalah penggabungan antara beberapa persegi yang tumpang tindih. Bangun ini sering digunakan dalam seni dan desain grafis untuk menciptakan efek visual yang menarik. Luasnya akan tergantung pada cara persegi-persegi tersebut tumpang tindih.
- Segi Enam
Segi enam adalah bangun datar yang memiliki enam sisi dan enam sudut. Segi enam bisa bersifat reguler (sisi dan sudutnya sama) atau tidak. Luas segi enam reguler dapat dihitung dengan rumus L = (3√3/2) s², di mana s adalah panjang sisi. Segi enam banyak digunakan dalam desain arsitektur dan cukup populer dalam dunia permainan seperti catur.
- Oval
Oval adalah bangun datar yang menyerupai bentuk lingkaran tetapi tidak sepenuhnya bulat. Oval tidak memiliki formula khusus untuk menghitung luasnya, namun dapat diasumsikan dengan menghitung luas lingkaran yang lebih besar dengan mengalikan faktor tertentu. Oval bisa kita temui dalam bentuk desain logo dan di berbagai artefak seni.
Dalam kesimpulannya, bangun datar adalah bagian fundamental dari geometri yang tidak hanya membawa pengetahuan teoritis, tetapi juga aplikasi praktis yang ditemukan dalam kehidupan sehari-hari. Memahami berbagai jenis bangun datar membantu kita dalam mengenali bentuk-bentuk di sekitar kita serta memberikan dasar yang kuat dalam membaca dan menganalisis masalah matematika lebih lanjut. Dengan mengetahui karakteristik masing-masing bangun datar, kita dapat meningkatkan keterampilan analitis dan pemecahan masalah. Semoga penjelasan mengenai sepuluh bangun datar ini dapat menambah wawasan dan pengetahuan pembaca akan dunia matematika yang penuh dengan keindahan dan logika.